Các thuật toán sắp xếp phổ biến
Sắp xếp là sắp đặt các phần tử của một cấu trúc theo thứ tự tăng dần (hay giảm dần). Với một cấu trúc đã được sắp xếp chúng ta rất thuận tiện khi thực hiện các tác vụ trên cấu trúc như tìm kiểm, trích lọc, duyệt cấu trúc ….
Giới thiệu
Sắp xếp là sắp đặt các phần tử của một cấu trúc theo thứ tự tăng dần (hay giảm dần). Với một cấu trúc đã được sắp xếp chúng ta rất thuận tiện khi thực hiện các tác vụ trên cấu trúc như tìm kiểm, trích lọc, duyệt cấu trúc ….
Có 2 loại giải thuật sắp xếp được dùng phổ biến trong khoa học máy tính là internal sorting và external sorting
- Với internal sorting thì toàn bộ dữ liệu cần sắp xếp được đưa vào bộ nhớ trong, do vậy kich thước dữ liệu cần sắp xếp nhỏ và thời gian sắp xếp được thực hiện rất nhanh.
- Với external sorting thì chỉ một phần nhỏ dữ liệu cần sắp xếp được đưa vào bộ nhớ trong, phần lớn dữ liệu còn lại được lưu ở bộ nhớ ngoài , kích thước dữ liệu cần sắp xếp lúc này rất lớn, và thời gian sắp xếp thực hiện rất chậm.
Trong khuôn khổ bài này mình chỉ xin giới thiệu về internal sorting để các bạn có một các nhìn khoa học hơn về giải thuật sắp xếp. Internal sorting bao gồm:
- Bubble sort.
- Quick sort.
- Simple selection sort.
- Heap sort.
- Simple insertion sort.
- Shell sort.
- Merge sort.
- Radix sort.
Chúng ta sẽ đi từng phần cụ thể nhé.
Đầu tiên chúng ta sẽ tạo ra 1 mảng dữ liệu test như sau
// Sort the original data
private static final int [] NUMBERS =
{ 49 , 38 , 65 , 97 , 76 , 13 , 27 , 78 , 34 , 12 , 64 , 5 , 4 , 62 , 99 , 98 , 54 , 56 , 17 , 18 , 23 , 34 , 15 , 35 , 25 , 53 , 51 };
Bubble sort (sắp xếp bằng cách đổi chỗ)
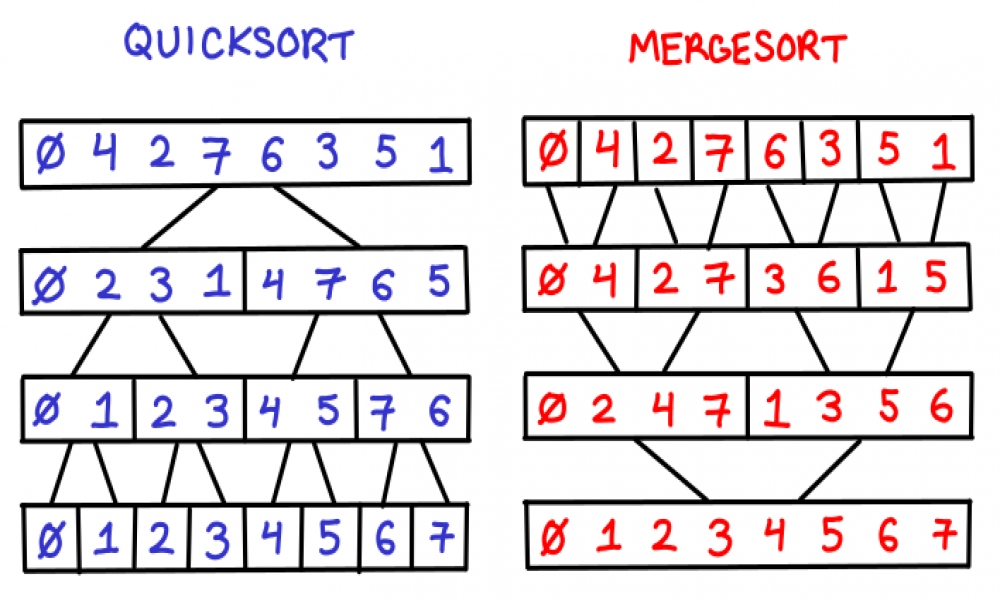
Nhìn vào hình mô tả bên trên chắc các bạn đã hình dung ra các mà phương pháp này sử dụng để sắp xếp các phần như nào rồi nhỉ. Phương pháp này sẽ duyệt danh sách nhiều lần, trong mỗi lần duyệt sẽ lần lượt so sánh cặp nút thứ i và thứ i+1 và đổi chỗ hai nút này nếu chúng không đúng thứ tự. Sau đây là code cài đặt giải thuật bubble sort.
public static void bubbleSort ( int [] array) {
int temp = 0 ;
for ( int i = 0 ; i <array.length - 1 ; i ++) {
for ( int j = 0 ; j <array.length - 1 - i; j ++) {
if (array [j]> array [j + 1 ]) {
temp = array [j];
array [j] = array [j + 1 ];
array [j + 1 ] = temp;
}
}
}
System.out.println (Arrays.toString (array) + "bubbleSort" );
}
Quick Sort — Sắp xếp nhanh
Quick sort là phương pháp đổi chỗ từng phần (partition exchange), đây là phương pháp rất hiệu quả, rất thông dụng..
Nội dung của phương pháp này như sau:
Chọn một nút bất kỳ trong danh sách(Giả sử là nút số 5 như trên hình) gọi là nút làm trục (pivot node), xác định vị trí hợp lệ của nút này trong danh sách (gọi là vị trí pivot).
Tiếp theo chúng ta phân hoạch các nút còn lại trong danh sách cần sắp xếp sao cho từ vị trí 0 đến vị trí pivot-1 đều có nội dung nhỏ hơn hoặc bằng nút làm trục, các nút từ vị trí pivot+1 đến n-1 đều có nội dung lớn hơn nút làm trục.
Quá trình lại tiếp tục như thế với hai danh sahs con từ trị trí 0 đến vị trí pivot-1 và từ vị trí pivot+1 đến vị trí n-1, … Sau cùng chúng ta sẽ được danh sách có thứ tự. Sau đây là code cài đặt giải thuật quick sort.
public static void quickSort(int[] array) {
_quickSort(array, 0, array.length - 1);
System.out.println(Arrays.toString(array) + " quickSort");
}
private static int getMiddle(int[] list, int low, int high) {
int tmp = list[low];
while (low < high) {
while (low < high && list[high] >= tmp) {
high--;
}
list[low] = list[high];
while (low < high && list[low] <= tmp) {
low++;
}
list[high] = list[low];
}
list[low] = tmp;
return low;
}
private static void _quickSort(int[] list, int low, int high) {
if (low < high) {
int middle = getMiddle(list, low, high);
_quickSort(list, low, middle - 1);
_quickSort(list, middle + 1, high);
}
}
Simple selection sort
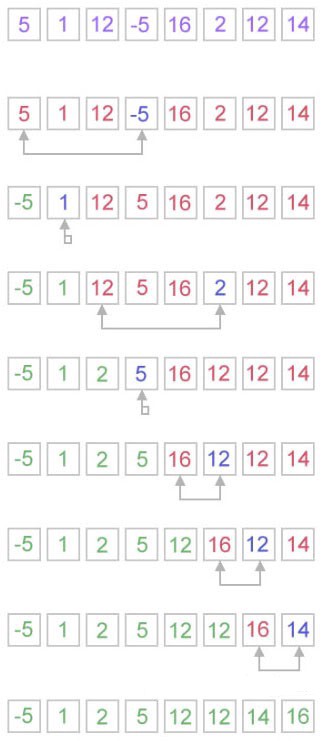
Ý tưởng thuật toán selection sort là: Chọn phần tử nhỏ nhất trong n phần tử ban đầu, đưa phần tử này về vị trí đúng là đầu tiên của dãy hiện hành. Sau đó không quan tâm đến nó nữa, xem dãy hiện hành chỉ còn n-1 phần tử của dãy ban đầu, bắt đầu từ vị trí thứ 2. Lặp lại quá trình trên cho dãy hiện hành đến khi dãy hiện hành chỉ còn 1 phần tử. Dãy ban đầu có n phần tử, vậy tóm tắt ý tưởng thuật toán là thực hiện n-1 lượt việc đưa phần tử nhỏ nhất trong dãy hiện hành về vị trí đúng ở đầu dãy.
public static void selectSort ( int [] array) {
int position = 0 ;
for ( int i = 0 ; i <array.length; i ++) {
int j = i + 1 ;
position = i;
int temp = array [i];
for (; j <array.length; j ++) {
if (array [j] <temp) {
temp = array [j];
position = j;
}
}
array [position] = array [i];
array [i] = temp;
}
System.out.println (Arrays.toString (array) + "selectSort" );
}
Heap Sort
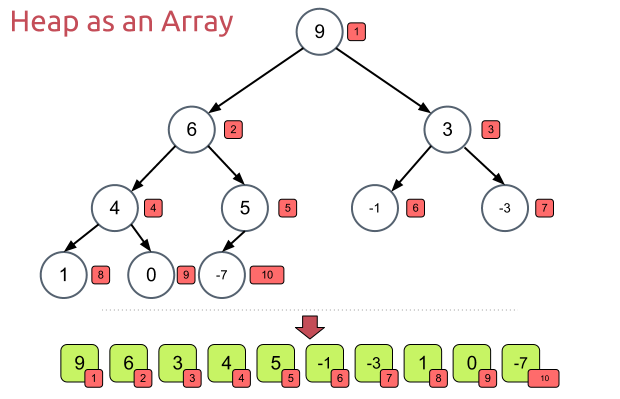
public static void heapSort(int[] array) {
int len = array.length - 1;
int beginIndex = (len - 1) >> 1;
for (int i = beginIndex; i >= 0; i--) {
maxHeapify(i, len, array);
}
for (int i = len; i > 0; i--) {
swap(0, i, array);
maxHeapify(0, i - 1, array);
}
System.out.println(Arrays.toString(array) + " heapSort");
}
private static void swap(int i, int j, int[] arr) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
private static void maxHeapify(int index, int len, int[] arr) {
int li = (index << 1) + 1;
int ri = li + 1;
int cMax = li;
if (li > len) {
return;
}
if (ri <= len && arr[ri] > arr[li])
{ cMax = ri; }
if (arr[cMax] > arr[index]) {
swap(cMax, index, arr);
maxHeapify(cMax, len, arr);
}
}
Simple insertion sort
.png)
Insertion sort là một thuật toán sắp xếp đơn giản, nó tạo ra mảng được sắp xếp cuối cùng một phần tử một lúc. Nó kém hiệu quả đối với mảng dữ liệu lớn so với các thuật toán sắp xếp khác.
Ưu điểm của Insertion Sort:
1) Giải thuật đơn giản, dễ implement
2) Nó rất hiệu quả cho các bộ dữ liệu nhỏ.
3) Tính ổn định cao
public static void insertSort ( int [] array) {
for ( int i = 1 ; i <array.length; i ++) {
int temp = array [i];
int j = i - 1 ;
for (; j> = 0 && array [j]> temp; j--) {
// Moves the value greater than temp back by one unit
array [j + 1 ] = array [j];
}
array [j + 1 ] = temp;
}
System.out.println (Arrays.toString (array) + "insertSort" );
}
Shell sort
.png)
Shell sort còn được gọi là sắp xếp tăng hẹp, nó là một insertion sort. Là một thuật toán bổ sung cho insertion sort.
Ý tưởng thuật toán:
Mỗi row được group bởi các step gap, mỗi group sử dụng insertion sort để sắp xếp, khi step gap giảm các group chứa được nhiều record hơn. Khi giá trị của gap được giảm xuống còn 1 toàn bộ dữ liệu được kết hợp thành một group để tạo thành một bộ dữ liệu đã được sắp xếp.
public static void shellSort ( int [] array) {
int i;
int j;
int temp;
int gap = 1 ;
int len = array.length;
while (gap <len / 3 ) {gap = gap * 3 + 1 ;}
for (; gap> 0 ; gap / = 3 ) {
for (i = gap; i <len; i ++) {
temp = array [i];
for (j = i - gap; j> = 0 && array [j]> temp; j - = gap) {
array [j + gap] = array [j];
}
array [j + gap] = temp;
}
}
System.out.println (Arrays.toString (array) + "shellSort" );
}
Merge sort
.png)
Các bước để implement Merge Sort:
1) Chia mảng dữ liệu chưa sort thành n phân vùng, mỗi phân vùng chứa 1 phần tử. Tại đây phần tử được coi đã được sắp xếp.
2) Lặp đi lặp lại các đơn vị được phân chia để tạo ra một mảng mới cho đến khi chỉ còn lại 1 mảng con. Cuối cùng chúng ta thu được một mảng đã sắp xếp.
public static void mergingSort ( int [] array) {
sort (array, 0 , array.length - 1 );
System.out.println (Arrays.toString (array) + "mergingSort" );
}
private static void sort ( int [] data, int left, int right) {
if (left <right) {
int center = (left + right) / 2 ;
sort (data, left, center);
sort (data, center + 1 , right);
merge (data, left, center, right);
}
}
private static void merge ( int [] data, int left, int center, int right) {
int [] tmpArr = new int [data.length];
int mid = center + 1 ;
int third = left;
int tmp = left;
while (left <= center && mid <= right) {
if (data [left] <= data [mid]) {
tmpArr [third ++] = data [left ++];
} else {
tmpArr [third ++] = data [mid ++];
}
}
while (mid <= right) {
tmpArr [third ++] = data [mid ++];
}
while (left <= center) {
tmpArr [third ++] = data [left ++];
}
while (tmp <= right) {
data [tmp] = tmpArr [tmp ++];
}
}
Radix sort
.png)
Radix Sort — Một thuật toán sắp xếp theo phương pháp cơ số không quan tâm đến việc so sánh giá trị của các phần tử như các thuật toán sắp xếp khác như Bubble sort, Selection sort, … Radix Sort sử dụng cách thức phân loại các con số trong dãy và thứ tự phân loại con con số này để tạo ra thứ tự cho các phần tử. Đây là cách tiếp cận khác so với các phương pháp sắp xếp khác.
public static void radixSort ( int [] array) {
int max = array [ 0 ];
for ( int i = 1 ; i <array.length; i ++) {
if (array [i]> max) {
max = array [i];
}
}
int time = 0 ;
while (max> 0 ) {
max / = 10 ;
time ++
}
ArrayList <ArrayList <Integer >> queue = new ArrayList <> ();
for ( int i = 0 ; i < 10 ; i ++) {
ArrayList <Integer> queue1 = new ArrayList <> ();
queue.add (queue1);
}
for ( int i = 0 ; i <time; i ++) {
for ( int anArray: array) {
int x = anArray% ( int ) Math.pow ( 10 , i + 1 ) / ( int ) Math.pow ( 10 , i);
ArrayList <Integer> queue2 = queue.get (x);
queue2.add (anArray);
queue.set (x, queue2);
}
int count = 0 ;
for ( int k = 0 ; k < 10 ; k ++) {
while (queue.get (k) .size ()> 0 ) {
ArrayList <Integer> queue3 = queue.get (k);
array [count] = queue3.get ( 0 );
queue3.remove ( 0 );
count ++;
}
}
}
System.out.println (Arrays.toString (array) + "radixSort" );
}

Theo dõi VnCoder trên Facebook, để cập nhật những bài viết, tin tức và khoá học mới nhất!
Bài viết mới

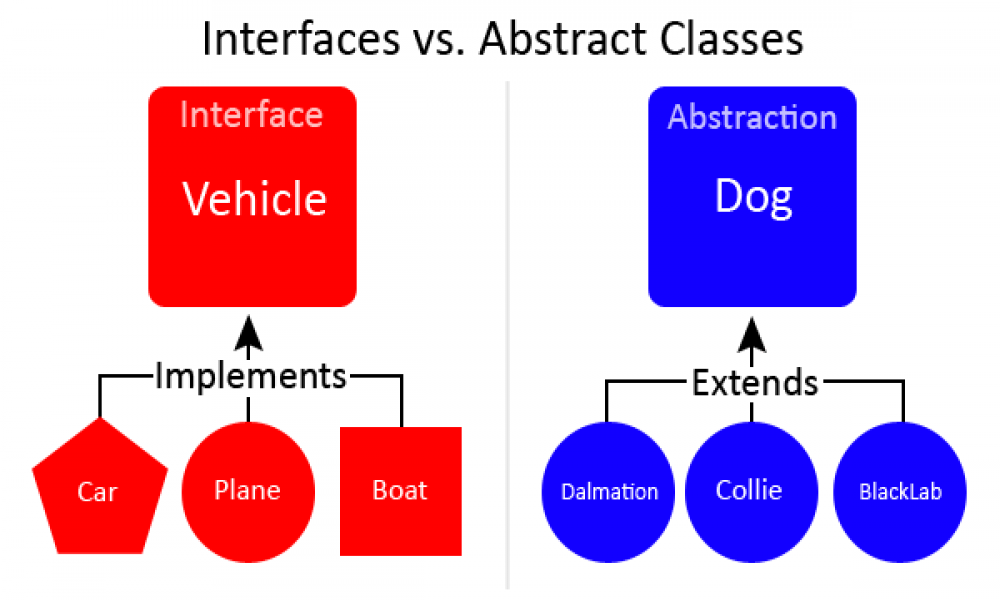
Interface là gì? Interface khác gì Class? Đa kế thừa trong Java sử dụng Interface như thế nào? Ví dụ minh họa
Abstract Class (Lớp trừu tượng) là gì? Abstract Method (Phương thức trừu tượng) trong là gì? Các ví dụ minh họa trong Java.
Upcasting, Dowcasting là gì? Cơ chế chuyển kiểu đối với kiểu dữ liệu tham chiếu (Ép kiểu đối tượng) trong Java

.png)